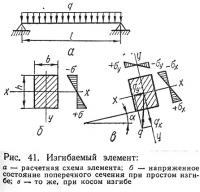
Различают два вида работы элементов на изгиб — (рис. 41, а): простой изгиб, когда нагрузка действует в плоскости одной из главных осей инерции поперечного сечения элемента (рис. 41, б); косой изгиб, когда направление нагрузки не совпадает ни с одной из главных осей инерции сечения (рис. 41, в).
Расчет элементов на прочность при простом изгибе производится по формуле

где М — расчетный изгибающий момент, кН·см;
mи — коэффициент условий работы элемента при изгибе, принимаемый равным 1, за исключением случаев введения поправок на форму и размеры сечения (например mб и mгн для расчета клееных прямолинейных и гнутых элементов);
Wvac4 — расчетный момент сопротивления (по площади нетто) рассматриваемого поперечного сечения, см3;
Rи — расчетное сопротивление материала изгибу, МПа.
Подбор сечения по заданному расчетному изгибающему моменту М при простом изгибе производится по формуле
По найденному моменту сопротивления находятся размеры поперечного сечения и подбирается пиломатериал по сортименту. Например, для прямоугольного сечения

Пиломатериал подбирается так, чтобы принятое сечение имело Wпр>Wтр.
Расчет элементов на прочность по нормальным напряжениям при косом изгибе производится по формуле
где σх я σу — соответствующие моментам Мх и Му напряжения изгиба;
Мх и Мg — составляющие расчетного изгибающего момента относительно главных осей х и у;
Wx и Wy — расчетные моменты сопротивления рассматриваемого поперечного сечения для осей х и у;
Rи — расчетное сопротивление материала изгибу.
Для подбора сечения при косом изгибе формулу (30) можно преобразовать:
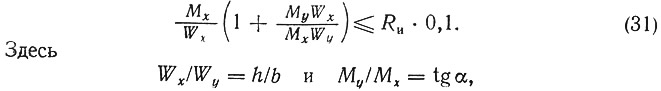
если сечение прямоугольное и пролеты изгибаемого элемента относительно осей х и у одинаковы. Подставляя эти величины в формулу (31) и решая ее относительно Wx, получим:
Расчет изгибаемых элементов на скалывание производится в местах наибольших поперечных сил (обычно — возле опор) по формуле

где Q — расчетная поперечная сила в данном сечении, кН;
Sбр, см3 и Iбр, см4 — статический момент брутто и момент инерции брутто сдвигаемой части сечения относительно нейтральной оси;
bрасч — расчетная ширина сечения, см;
Rcк — расчетное сопротивление материала скалыванию при изгибе, МПа.
Проверка на скалывание при изгибе цельных деревянных элементов может оказаться решающей для коротких балок (l/h≤5) с большими нагрузками или для балок с двумя сосредоточенными силами возле опор. Для балок цельного сечения покрытий и перекрытий зданий с равномерной нагрузкой проверку на скалывание можно не проводить.
Для изгибаемых элементов из конструкционных пластмасс проверка на скалывание обязательна.
Проверка жесткости изгибаемого элемента состоит в определении наибольшего изгиба от нормативных нагрузок и в сопоставлении его с предельно допустимым (см. приложение 5). Обычно прогиб вычисляется как относительная величина f/l в предположении упругой работы древесины. Влиянием касательных напряжений на прогиб балок прямоугольного сечения обычно пренебрегают и учитывают его лишь при расчете клеедощатых балок таврового сечения с тонкими стенками.
Вычисление прогибов производится по формулам сопротивления материалов в соответствии с расчетными схемами. Для балок симметричного сечения в плоскости изгиба прогибы можно находить по обобщенной формуле
где σн — максимальное напряжение от нормативной нагрузки, МПа;
k — коэффициент, зависящий от условий опирания и нагрузки; находится по справочной литературе, например, для балки на двух опорах при равномерной нагрузке k = 5/24; для такой же балки со сосредоточенной силой по середине пролета k = 1/6 и т. д.
При подборе сечения по условию жесткости необходимую высоту балки получаем из выражения (34), приравнивая его предельному прогибу:
Заменяем напряжения от нормативной нагрузки на напряжения от расчетной нагрузки σн = σ/nср (здесь nср — усредненный коэффициент перегрузки). Тогда при полном использовании прочности материала — σ = R, получим оптимальную высоту поперечного сечения балки
Проверка жесткости при косом изгибе производится по полному прогибу, равному геометрической сумме прогибов fx и fy:
где fx — прогиб относительно оси х;
fy — прогиб относительно оси у.
Косой изгиб всегда вызывает увеличение размеров изгибаемых элементов, поэтому следует стремиться к его исключению или ограничению, например, постановкой тяжей в плоскости ската крыши по середине пролета прогонов, уменьшая тем самым в два раза расчетный пролет в плоскости ската.
Расчет пластмассовых элементов на изгиб производится по общим правилам расчета изгибаемых элементов. Особенностью конструкционных пластмасс является то, что многие из них имеют высокую прочность R при малом модуле упругости Е. Поэтому при расчете на изгиб стеклопластиковых балок решающей часто оказывается проверка по второму предельному состоянию. Но в этом случае материал в элементах невозможно полностью использовать по прочности, так как при этом нарушаются пределы его деформирования. Для уменьшения этого экономически невыгодного явления сечениям изгибаемых элементов стремятся придать форму, которая увеличивает геометрические характеристики сечения I и W при одном и том же значении F, например, применяя в балках коробчатые, двутавровые, швеллерные и другие профильные сечения вместо сплошных прямоугольных.
Другой особенностью работы изгибаемых пластмассовых элементов является существенное влияние сдвига на прогиб. Этот дополнительный прогиб, как правило, пропорционален квадрату отношения высоты балки к пролету и соотношению модулей нормальной упругости и сдвига. Жесткость изгибаемых пластмассовых элементов проверяется по формуле
где f/l — относительный прогиб, найденный без учета сдвига;
G — модуль сдвига, принимаемый равным E/12(1+μ);
kсд — коэффициент сдвига, зависящий от формы сечения и расчетной схемы балки; например, для прямоугольной балки свободно опертой при равномерной нагрузке kсд = 0,96, а при сосредоточенной силе в середине пролета kсд = 1,2.