Проверку прочности стержня делают в наиболее ослабленном сечении по формуле
Устойчивость стержня проверяется по формуле
В этих формулах N — расчетное продольное усилие, действующее на элемент, кН;
mс — коэффициент условия работы элемента на сжатие, принимаемый равным 1;
Rc — расчетное сопротивление материала сжатию, МПа;
Fнт = (Fбр—Fосл) — площадь сечения нетто, определяемая как для растянутого элемента, см2;
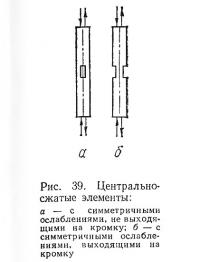
Fрасч — расчетная площадь поперечного сечения элемента при проверке устойчивости, см2, принимаемая: при отсутствии ослаблений — Fрасч = Fбр; при ослаблениях, не выходящих на кромку (рис. 39, а), если площадь ослаблений не превышает 25% от площади Fбр, то Fрасч = Fбр; если площадь ослаблений превышает 25% площади Fбр, то Fрасч = (3/4)Fнт; при симметричных ослаблениях, выходящих на кромку (рис. 39, б) — Fрасч = Fнт.
При несимметричных ослаблениях, выходящих на кромку, элементы рассчитываются как внецентренно сжатые.
Входящий в формулу (16) коэффициент продольного изгиба φ представляет собой отношение критического напряжения (т. е. напряжения, при котором стержень теряет устойчивость) к пределу прочности материала на сжатие — σкр/Кспр. Коэффициент φ обычно меньше единицы (или равен единице), что свидетельствует о неполном использовании прочностных свойств материала. При проектировании целесообразно по возможности предусматривать меры по обеспечению устойчивости сжатых стержней. Коэффициент φ зависит от гибкости стержня λ. Для стержней из различных материалов установлены граничные значения гибкостей λмин, при повышении которых элемент работает в пределах пропорциональности, а при меньших значениях за пределом пропорциональности.
При работе элемента до условного предела пропорциональности при λ>λмин коэффициент φ находится по формуле Эйлера

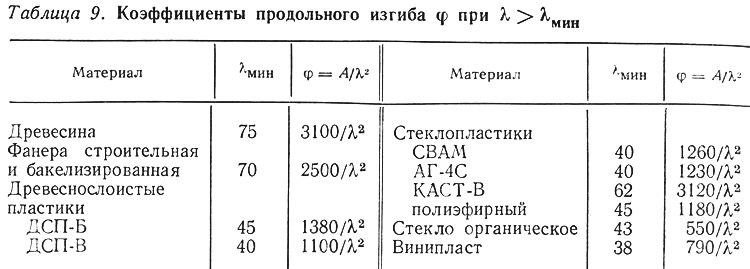
Результаты испытаний показывают, что отношение модуля упругости к пределу прочности для большинства материалов можно принять постоянным. Затем в формуле (17) значение π2E/Rпр заменяется на постоянную величину для материала — А и коэффициент продольного изгиба находится по формулам, приведенным в табл. 9.
При работе элементов за пределами пропорциональности коэффициенты φ определяются по следующим формулам, полученным на основании экспериментальных данных: для деревянных элементов при λ≤75
для фанерных элементов при λ≤70
для всех стеклопластиков при λ≤λмин
где Rп.п — условный предел пропорциональности;
Rт — условный предел текучести.
По результатам исследований ЛИСИ для расчета элементов из фанерных труб, швеллеров и уголков можно применять следующие формулы для определения коэффициентов продольного изгиба:

При расчете элементов трубчатого сечения (стеклопластиковых и фанерных), кроме проверки общей устойчивости, проверяется устойчивость стенки трубы по условию
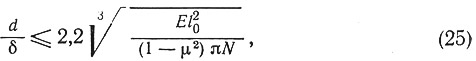
где d — диаметр осевой линии стенки трубы;
δ — толщина стенки трубы;
l0 — расчетная длина элемента;
μ — коэффициент Пуассона.
Гибкости элементов λ определяются в зависимости от их расчетной длины и радиуса инерции поперечного сечения по формуле
и не должны превышать предельных значений, приведенных в приложении 4.
Расчетная длина элемента зависит от способа закрепления его концов и равна l0 = lμ', где l — геометрическая длина. Значения коэффициента μ' для различно закрепленных стержней приведены на рис. 40, здесь же показаны формы искривления стержней при потере ими устойчивости. Для элементов из дерева и фанеры при наличии защемления на концах значение μ' несколько больше, чем для пластмассовых элементов, так как вследствие поперечного обжатия или усушки древесины полное защемление затруднительно.