Таблицы для гидравлического расчета самотечных трубопроводов [14, 26] не всегда дают возможность произвести достаточно точные расчеты. Таблицы в работе [14] составлены только для бетонных и железобетонных труб с шероховатостью n=0,014 и для квадратичной области турбулентного течения жидкости, а таблицы в работе [26] — для чугунных канализационных труб с шероховатостью n=0,013. Эти данные для переходной области турбулентного течения не дают достоверного результата.
Необходимость гидравлического расчета самотечных трубопроводов в каждом конкретном случае требует упрощения и, самое главное, уточнения методики этого расчета.
Анализ известных зависимостей, в том числе и данных работ [14, 25], позволяет установить, что:
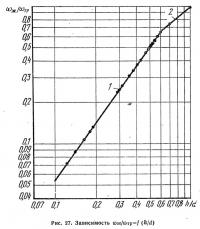
где ωж — площадь живого сечения потока жидкости в количестве qж, движущейся со скоростью vж, м2; ωтр — площадь живого сечения трубопровода диаметром d, м2; h — высота протекающего слоя жидкости, м.
Зависимость (83), представленная на рис. 27, может быть аппроксимирована прямыми 1 и 2. Первая из них описывается уравнением
а вторая:
Из уравнения (84)
Это равенство действительно при h/d от 0,1 до 0,6 включительно. При h/d>0,6 диаметр трубопровода можно найти из (85):
Для упрощения расчетов по формулам (86) и (87) канд. техн. наук Л. А. Шопенским разработана номограмма (рис. 28).
Следующим важным этапом расчетов является обоснование исходных параметров — наполнения трубопровода и скорости течения жидкости — для определения диаметра и уклона трубопровода.
Отметим, что в настоящее время гидравлический расчет трубопроводов производят по величине максимального секундного расхода сточной жидкости. Определение этой величины регламентировано действующими нормами СНиП П-30-76 «Внутренний водопровод и канализация зданий. Нормы проектирования» и базируется на вероятности действия санитарно-технических приборов, что справедливо только для систем водоснабжения, характеризующихся неразрывностью потока воды. Однако в системах канализации зданий преобладают залповые поступления жидкости, трубопроводы же имеют значительную аккумулирующую емкость, что способствует резкому снижению но длине трубопровода величины секундного расхода жидкости, первоначально поступающей в него.
Экспериментальные исследования влияния аккумулирующей способности канализационных трубопроводов на формирование секундных расходов жидкости выполнены в ЦНИИЭП инженерного оборудования на гидравлическом стенде, на котором поочередно монтировались трубопроводы длиной до 15 м из стеклянных труб диаметрами 79 и 104 мм и чугунных битуминизированных труб диаметром 96 мм. Станина стенда имеет опоры, позволяющие изменять уклон трубопровода. Моделирование-залповых сбросов сточных вод проводилось с помощью установленных на верхнем участке стенда шести унитазов «Компакт» с бачками емкостью 6,5—7 л. При одновременной работе шести унитазов максимальный секундный расход сточной жидкости составлял 9,6 л/с, что эквивалентно расходу стоков от 210 типовых квартир. Емкость трубопровода постоянного диаметра изменялась путем изменения его длины.
Секундный расход жидкости определялся с помощью мерной емкости, представляющей собой цилиндр диаметром 2 м, разделенный на 60 равных секторов, по методике, изложенной выше.
Экспериментальные исследования подтвердили, что канализационные трубопроводы обладают значительной аккумулирующей способностью. Так, например, при одновременном опорожнении шести унитазов в отводной горизонтальный трубопровод диаметром 104 мм, проложенный с уклоном 0,026, максимальный расход жидкости в конце участка длиной 11,6 м составил 3,6 л/с вместо 9,6 л/с, который поступал в начале трубопровода.
Зависимости для определения расчетного секундного расхода жидкости qрасч, л/с, получены с учетом таких параметров, как диаметр, длина, шероховатость, уклон трубопровода, угол входа в него жидкости.
При длине трубопровода, равной или более 3 м:
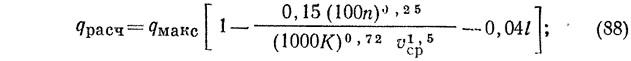
при длине трубопровода менее 3 м
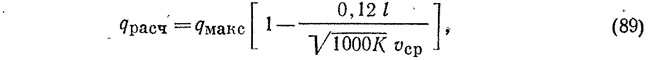
где qмакс — максимальный секундный расход сточной жидкости, определяемый по методике СНиП Н-30-76, л/с: n — коэффициент шероховатости материала трубопровода; К — параметр, зависящий от наполнения трубопровода и определяемый по табл. 15; vср — средняя скорость течения, м/с; l — длина трубопровода, м.

Следует отметить, что величина секундного расчетного расхода окончательно формируется на длине трубопровода, примерно равной 110 его диаметрам, т. е. на этой длине секундный расход становится минимальным и постоянным. Поэтому при расчетах по формуле (88) следует принимать l равной 110 диаметрам трубопровода в тех случаях, когда фактическая длина больше или равна этой величине; если же она меньше 110 d, следует принимать фактическую длину.
Транспортирующая способность жидкости применительно к специфике канализационных выпусков из зданий исследовалась в ЦНИЙЭП инженерного оборудования инж. В. Н. Родиным [19]. При исследовании использовались в виде включений структурные и волокнистые материалы различной крупности и плотности. Трубопровод помещался на металлическую станину, уклон которой определялся по нивелиру. Верхний конец трубопровода при помощи мягкой резины был закреплен в патрубке бака емкостью 0,3 м3, установленного на верхнем участке стенда. В этот бак из системы водоснабжения подавалась вода. Из трубопровода вода поступала во второй бак, откуда отводилась на сброс. Исследования проводились на трубопроводах диаметрами 57, 79, 104 мм, проложенных с уклонами в пределах от 0,01 до 0,04. Длина трубопроводов 12 м. Расход воды на выходе из трубопровода определялся объемным способом, высота слоя воды в трубопроводе — с помощью мановакуумметров, установленных через каждые 3 м, а также на выходе из трубопровода (мерным щупом). Средняя скорость течения жидкости определялась из условия неразрывности потока.
Образцы материала, применявшиеся при исследовании транспортирующей способности, помещались в верхнюю часть трубопровода, затем из бака подавалась вода, расход которой увеличивался до того момента, когда образец начинал двигаться. При этом фиксировались расход воды и наполнение трубопровода.
В результате исследований было установлено, что для транспортирования крупногабаритных предметов наполнение трубопровода имеет не меньшее значение, чем скорость течения жидкости. В частности, ветошь (во многих случаях являющаяся причиной засоров во внутридомовых системах канализации) транспортируется, если полностью погружена в воду, хотя скорость течения при этом равна 0,35—0,4 м/с, а песок крупностью 2,5 мм — при скорости 0,6—0,7 м/с.
На основе комплекса исследований, а также анализа статистики засоров за 30 лет В. Н. Родиным рекомендовано следующее условие, обеспечивающее нормальную работу канализационных выпусков из зданий: vср√
На необходимость увеличения наполнения трубопровода указывает д-р техн. наук Г. Г. Шигорин в работе [28], в которой отмечается, что при недостаточном наполнении трубопровода в нем начинают откладываться в первую очередь крупногабаритные предметы, причем высокие скорости течения жидкости не препятствуют этому процессу. В результате через 4—6 мес образуются засоры на трубопроводах диаметрами 200 и даже 250 мм.
По данным НИИ коммунального водоснабжения и очистки воды Академии коммунального, хозяйства им. К. Д. Памфилова, наполнение трубопровода является важным фактором, препятствующим отложению осадка в самотечных трубопроводах. Данные по 17 городам РСФСР представлены в табл. 16.

Последним этапом расчетов является определение уклона трубопровода.
Исследования позволили нам способом подбора для трубопроводов с n=0,012—0,014 аппроксимировать (с точностью в пределах 7—10%) формулы Шези — Н. Н. Павловского зависимостью:
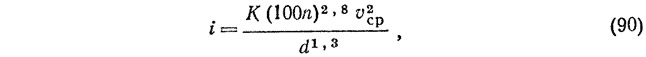
где К — коэффициент пропорциональности, зависящий от наполнения трубопровода (см. табл. 15).
Однако эта зависимость может быть рекомендована только для квадратичной области турбулентного течения жидкости, когда сопротивление движению пропорционально скорости во второй степени и не зависит от числа Рейнольдса.
Для разработки методики гидравлического расчета самотечных труб и каналов во всей области турбулентного течения жидкости нами выполнены аналитические и экспериментальные исследования. Аналитические исследования базируются на связи между законом гидравлического сопротивления и распределением скоростей по сечению труб и каналов.
Анализ зависимостей Шези — Н. Н. Павловского позволил представить основное уравнение равномерного установившегося движения жидкости
где Rv макс—гидравлический радиус, соответствующий расстоянию точки потока, движущегося с максимальной скоростью, от стенки, в новой интерпретации
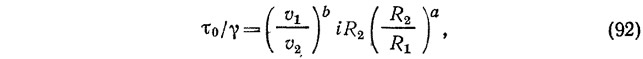
здесь τ0 — среднее касательное напряжение трения на стенке для данного поперечного сечения канала, кгс/см2; γ — объемная масса жидкости, кг/м3; v1 и v2 — скорости течения жидкости, м/с, — средние при разных наполнениях канала, осредненные — при постоянном наполнении; R1 и R2 — гидравлические радиусы, соответствующие точкам потока, в которых скорости равны v1 и v2, м; i — потери напора; b — показатель степени, характеризующий режим течения жидкости (для ламинарного режима b=1; для переходной области турбулентного режима b=1—2; в квадратичной области b=2); а — показатель степени, характеризующий материал труб и каналов и для безнапорных потоков равный 2у в формуле Н. Н. Павловского (3). Для напорных потоков а определяется по другой зависимости.
На основе экспериментальных данных Н. Н. Павловского, И. Никурадзе, Ф. А. Шевелева, МИСИ им. В. В. Куйбышева по изменению скоростей в сечениях напорных и безнапорных труб и каналов установлено, что в переходной области турбулентного течения жидкости
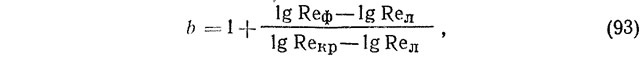
где Reл — максимальное число Рейнольдса при ламинарном режиме (Refl=2400);
Reкр — критическое число Рейнольдса, соответствующее началу квадратичной области сопротивлений:
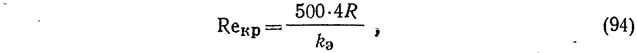
здесь kэ — эквивалентная шероховатость материала труб и каналов, мм (табл. 17);
Reф — число Рейнольдса, фактическое;
здесь v — кинематическая вязкость жидкости, м2/с.

Совместное решение уравнений (91) и (92) позволяет получить следующие зависимости:
для профиля осредненных скоростей в напорном потоке
где λ — коэффициент сопротивления Дарси;
отношение средних скоростей в безнапорном потоке
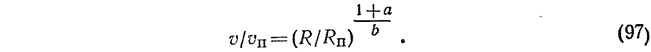
Формула (96) описывает нижнюю ветвь осесимметричной параболы (профиль скоростей в напорных потоках), имеющей максимум на оси трубы; верхняя ветвь параболы является зеркальным отображением ее нижней ветви.
Формула (97) описывает отношение средних скоростей по всему сечению безнапорного потока, в котором vп и Rп — скорость течения и гидравлический радиус при полном наполнении.
Точность расчетов по формуле (97) можно проиллюстрировать на примере графика «рыбка», впервые приведенного акад. Н. Н. Павловским и в дальнейшем многократно повторенного в различных курсах и монографиях по гидравлике и канализации (табл. 18).
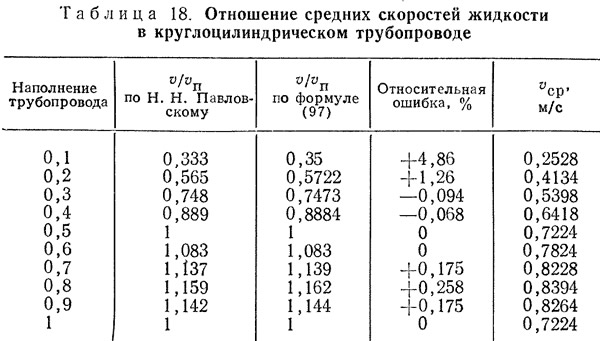
Это отношение средних скоростей не подчиняется закону Шези и, следовательно, может иметь место лишь в переходном режиме турбулентного течения жидкости. В частности, данные табл. 18 рассчитаны для асфальтированного чугунного трубопровода (n=0,012, а=0;28) диаметром 100 мм при b=1,6717 (Reп=72240).
Отметим также, что формула (97) с достаточной степенью точности описывает отношение средних скоростей в самотечных каналах некруглой формы поперечного сечения, а формула (96) — профили осредненных скоростей в напорных потоках, полученные И. Никурадзе, МИСИ им. В. В. Куйбышева, Ф. А. Шевелевым.
Следует указать, что структура формулы для определения коэффициента гидравлического сопротивления, самотечных трубопроводов отлична от структуры формул для расчета напорных трубопроводов. Это объясняется тем, что в напорных трубопроводах расчет производят по средней скорости, определяемой как частное от деления величины расхода жидкости на площадь сечения трубопровода. Единственному значению скорости течения соответствует единственное значение коэффициента сопротивления λ, и потери напора определяют по формуле Дарси — Вейсбаха
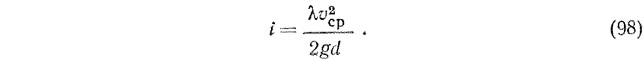
При безнапорном течении каждому новому наполнению трубопровода соответствуют: новая скорость течения, новый коэффициент λ и новое значение гидравлического радиуса R, но при этом должно соблюдаться условие
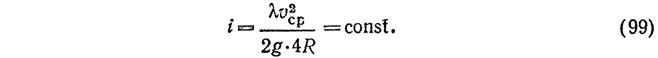
Отсюда закон распределения коэффициента λ по сечению безнапорного трубопровода (канала):
Этот закон и отношение средних скоростей по сечению канала позволяют получить формулу для определения потерь напора во всей области турбулентного течения жидкости.
На основании анализа для безнапорного течения можно рекомендовать следующую зависимость для определения коэффициента λ:
Коэффициент 0,2 обеспечивает одинаковое, значение эквивалентной шероховатости напорных и безнапорных трубопроводов, выполненных из одного и того же материала.
При подстановке этого значения λ в формулу (98) достигается результат, практически точно совпадающий с результатом расчетов по формулам Шези — Павловского.
Из формулы (101) следует:
С учетом (97) уравнение (102) примет вид:
При b=2 условие (103) отвечает условию (100). Отсюда следует, что в квадратичном режиме учитываются оба названных закона. При b≠2 условие (100) не соблюдается, что обусловливает парадоксальное явление, при котором, расчетный уклон одного и того нее трубопровода изменяется при изменении его наполнения. Проиллюстрируем это на примере расчета стального трубопровода диаметром 100 мм по формуле СНиП 11-32-74 при Reп=15 310 (табл. 19).
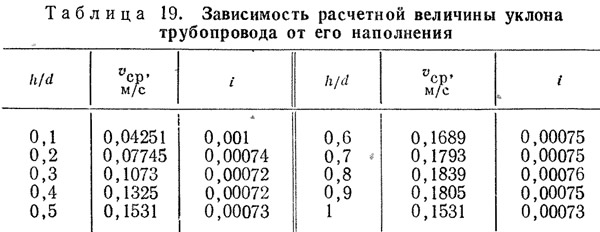
Из приведенных в табл. 19 данных следует, что при изменении наполнения трубопровода от 0,1 до 0,4 его расчетный уклон изменяется на 28%. Это указывает на недостоверность расчетной формулы.
Наиболее простым решением для определения потерь напора, учитывающим законы изменения средних скоростей и коэффициента сопротивления по сечению канала, а также режим течения жидкости, является следующая интерпретация уравнения Дарси — Вейсбаха:
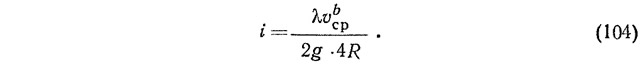
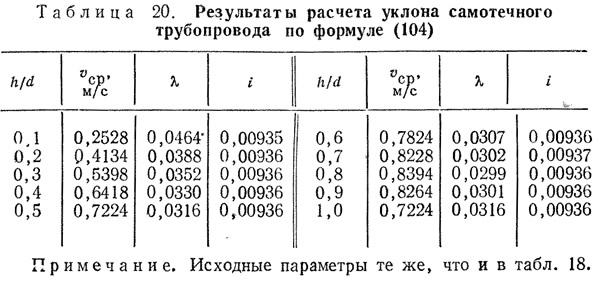
Зависимость (104) экспериментально проверена на гидравлическом стенде на трубопроводах из стеклянных и чугунных асфальтированных труб четырех диаметров, уклоны которых изменялись 14 раз. Результаты исследований позволяют констатировать достаточно высокую точность расчетов по формулам (93), (101) и (104) во всей области турбулентного течения жидкости. Эти формулы обеспечивают выполнение условия (99), о чем свидетельствуют данные табл. 20.
Уклон самотечного трубопровода канализационного выпуска из здания может быть определен также по номограмме (рис. 29).
Таким образом, для обеспечения необходимой величины транспортирующей способности потока сточной жидкости в канализационном выпуске из здания, он должен быть запроектирован на основании расчета, который состоит из следующих этапов:
- 1. Определение максимальной величины секундного расхода сточной жидкости по методике СНиП П-30-76;
- 2. Определение расчетного секундного расхода стоков по формуле (88) либо (89);
- 3. Выбор величины наполнения трубопровода и скорости течения жидкости из условия vср√
h/d ≥0,6; - 4. Определение диаметра трубопровода по номограмме (см. рис. 28). Если полученное значение диаметра не предусмотрено в сортаменте соответствующих труб, следует по сортаменту принять ближайший больший или меньший к расчетному диаметр и по той же номограмме уточнить величину наполнения трубопровода или скорость течения жидкости;
- 5. Определение уклона трубопровода на основании имеющихся данных, исходя из величины диаметра, наполнения и шероховатости трубопровода и скорости течения в нем жидкости.
Следует подчеркнуть, что на участках с небольшими расходами сточной жидкости необходимая величина транспортирующей способности потока сточной жидкости не может быть обеспечена. Такие участки канализационных выпусков следует считать безрасчетными, что должно быть отмечено в проекте, и предусматривать на них необходимое количество прочистных устройств. Эти участки должны находиться под постоянным наблюдением эксплуатирующих организаций.
Приведенная методика расчета канализационных выпусков из зданий позволяет снизить материалоемкость собственно выпусков до 40% и значительно уменьшить вероятность образования засоров.
Снижение стоимости строительства подземной части системы канализации здания может быть также достигнуто устройством торцевого выпуска, т. е. выпуска, объединяющего понизу все канализационные стояки в здании. Такое решение способствует увеличению секундного расхода сточной жидкости в выпуске и позволяет отказаться от устройства дворовой канализационной сети. Диаметр и уклон торцевого выпуска должны быть обоснованы расчетом.
Следует подчеркнуть, что при конструировании канализационных выпусков из зданий должно быть обеспечено максимальное уменьшение протяженности горизонтальных трубопроводов.