Согласно данным В.И. Заборова [5], приведенный уровень ударного звука под несущей частью перекрытия в общем случае определяется выражением
а для элементов сплошного сечения —
где q — поверхностная плотность плиты, кг/м2;
D — изгибная жесткость сечения, Па·м4;
η — коэффициент потерь;
ρ — плотность материала плиты, кг/м3;
Е — модуль упругости, Па, материала плиты;
h — толщина плиты, м.
Из формул (33) и (34) следует, что приведенный уровень ударного шума под однородной плитой зависит от частоты звука только в той мере, в какой изменяются с частотой параметры материала — модуль упругости и коэффициент потерь. У бетона частотная зависимость этих параметров незначительна, поэтому частотная характеристика приведенного уровня ударного шума должна приближаться к горизонтальной прямой. Местное смятие материала под молотком ударной машины приводит к увеличению времени контакта между молотком и конструкцией, что учитывается в теории. В частности, теоретическая модель, которая дает формулу (33), действительна на частотах, удовлетворяющих условию
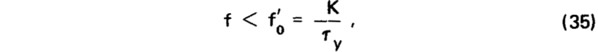
где f'0 — низшая собственная частота системы "молоток ударной машины — плита";
К — постоянная величина;
τу — время контакта молотка ударной машины с конструкцией при ударе (продолжительность удара), с.
С.Д. Ковригин, А.А. Маслов, В.М. Осадчиев установили [13], что формула (33) действительна только в диапазоне частот выше граничной частоты плиты fгр. Ими выведены зависимости для области частот f<fгр:
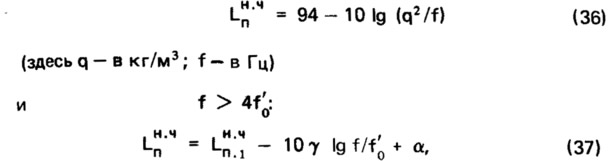
где γ — принимают равным от 2 до 5, а α — от 2,5 до 8,5 в зависимости от принятой модели соударения молотка ударной машины с поверхностью плиты;
Lн.чп.1 — величина, подсчитываемая по формуле (33).
Согласно изложенному, на частотах меньше fгр уровень ударного шума под перекрытием должен увеличиваться с темпом 3 дБ/окт, а на частотах, больших 4f'0 — уменьшаться (при увеличении частоты) с темпом 6—15 дБ/окт.
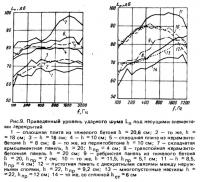
Частотные характеристики приведенного уровня ударного шума Lп однородных несущих элементов перекрытия различной конструкции (рис. 9), измеренные в жилых домах и на испытательном стенде ЦНИИЭП жилища (по данным автора), качественно согласуются с изложенными теоретическими представлениями. Однако величины Lп, вычисленные по формулам (33) и (34) при средних значениях параметров материала ρ, Е и η), значительно (почти на 10 дБ) Превышают экспериментальные. Сказывается то, что коэффициент потерь материала не отражает полного демпфирования плиты, обусловленного также потерями на границах конструкции. Частота f'0, после которой начинается уменьшение Lп, оказывается зависимой не только от материала плиты [13], но и от ее сечения. Объясняется это тем, что при тонкостенных элементах на Продолжительность удара заметное влияние оказывает прогиб тонкой плиты при ударе наряду с местным смятием. Рост Lп в нижней части нормируемого диапазона во многих случаях продолжается на частотах, значительно превышающих fгр.
Таким образом, непосредственное использование формул (33)—(37) для построения расчетных частотных характеристик приведенного уровня ударного шума не дает удовлетворительной сходимости с результатами эксперимента. Для более корректного построения такой характеристики необходимо учитывать фактическое демпфирование плиты в доме и влияние формы ее поперечного сечения на зависимость Lп от частоты.
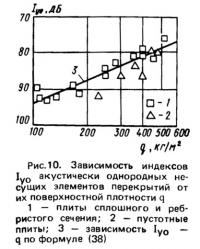
Частотная характеристика приведенного уровня ударного шума — промежуточный этап при определении индекса Iу. Проектировщику полезно иметь непосредственную зависимость индекса приведенного уровня ударного шума Iуо акустически однородных несущих элементов перекрытия от их поверхностной плотности q.
Экрпериментальная зависимость (рис. 10), полученная в результате испытаний на испытательном стенде ЦНИИЭП жилища и в натурных условиях [19], аппроксимирована формулой
Эта зависимость оказывается общей для плит сплошного и ребристого сечений из тяжелого и легкого бетонов [19]. Индексы плит с пустотами несколько большие, чем рассчитанные по формуле (38). Основной причиной, вызывающей повышение уровня ударного шума под пустотными плитами, можно считать резонансы воздуха в пустотах.
При укладке на бетонную несущую часть мягких покрытий пола (линолеумов на теплозвукоизолирующей подоснове, ковровых покрытий и т.д.) происходит значительная амортизация удара, связанная со смятием покрытия под молотком ударной машины и увеличением продолжительности удара. Теоретическое рассмотрение этого явления [5] позволяет получить следующее выражение для определения снижения уровня ударного шума при укладке на несущую часть перекрытия мягкого покрытия пола:
где f'0 — низшая собственная частота системы "молоток ударной машины — покрытие пола", зависящая от продолжительности удара:
Продолжительность удара τу нужно определять для каждого материала покрытия пола экспериментально. Использование связи между τу и глубиной вдавливания в покрытие штампа, находящегося под статической нагрузкой [11, 36], упрощает экспериментальное определение этой величины.
Как следует из формулы (39), снижение уровня ударного шума ΔLп должно равномерно расти с увеличением частоты с темпом 12 дБ/окт. Фактическое изменение ΔLп для линолеума на мягкой подоснове имеет более сложный характер, чем это следует из формулы (40), и только на отдельных участках может быть с достаточной точностью аппроксимировано этой формулой [14].
Практический метод расчета [9, 19, 39, 54] индекса Iу основан на использовании величин Iуо, подсчитанных по формуле (38), и ΔIу, определенных экспериментально для каждого вида покрытия пола. Изменение несущей части пола сравнительно мало влияет на частотную характеристику ΔLп, поэтому с достаточной точностью можно величины ΔIу, измеренные на одной конструкции несущей части, применять при расчете перекрытий с другими несущими частями. Используя их для расчета, необходимо учитывать снижение величины ΔIу при эксплуатации (см. п.4), а также при колебаниях характеристик материалов в процессе массового производства.
При теоретическом рассмотрении передачи ударного шума через перекрытие с раздельным полом [5] приняты две модели, в которых несущая часть перекрытия представлена в виде шарнирно-опертой по контуру прямоугольной плиты, а пол — в виде несвязанных между собой равномерно распределенных масс или в виде второй шарнирно-опертой по контуру прямоугольной плиты. Между полом и несущей частью перекрытия непрерывно и равномерно расположены безынерционные упругие поперечные связи. Первая модель принята для пола из мелкоразмерных слабосвязанных между собой элементов, вторая — для пола из крупных достаточно жестких элементов.
Согласно первой модели, снижение уровня ударного шума тем больше, чем больше отношение поверхностных плотностей пола и несущей части q2/q1 и чем ниже собственная частота пола f0, т.е. чем меньше жесткость звукоизоляционной прослойки. На достаточном удалении от f0 величина ΔLп растет при повышении частоты с темпом 12 дБ/окт. Для второй модели сохраняется та же закономерность, но она несколько усложнена влиянием отношения граничных частот несущей части и пола, которое зависит от отношения их поверхностных плотностей и жесткостей. Увеличение жесткости пола при прочих равных условиях приводит к уменьшению ΔLп.
Рассмотренные модели справедливы в области частот
где qc — поверхностная плотность упругого слоя (звукоизоляционной прослойки).
При более высоких частотах нельзя пренебрегать инерционностью упругого слоя. В этом диапазоне ΔLп растет при увеличении частоты с темпом 6 дБ/окт [5].
На приведенных результатах основан метод построения расчетной частотной характеристики ΔLп [50], которая состоит из двух отрезков прямой, имеющих уклоны 12—15 и 6 дБ/окт. Положение частотной характеристики в нормируемом диапазоне зависит от низшей собственной частоты пола и отношения поверхностных плотностей его и звукоизоляционной прослойки. Если низшая собственная частота пола попадает в нормируемый диапазон, то очертание кривой в непосредственной близости от нее принимают в зависимости от отношения поверхностных плотностей несущей части и пола. Этот метод [50] дает удовлетворительную сходимость с результатами натурных измерений, если основание пола выполнено из того же материала, что и несущая часть перекрытия (из бетона) . В случае деревянных полов расхождение между расчетными и измеренными индексами звукоизоляции достигает 6—16 дБ, причем при расчете получаются завышенные значения Iу. Это указывает на серьезные различия между параметрами теоретической модели, положенной в основу расчета, и реального пола на лагах.
Одним из факторов, обеспечивающих лучшую фактическую изоляцию ударного шума при деревянных полах, является значительная их податливость при ударе молотка ударной машины, что приводит к увеличению продолжительности удара. М.С. Терзибашьянц показал также [56], что при определении ΔLп в случае дощатого пола по лагам необходимо учитывать прохождение звука через лаги и через воздушный промежуток между ними.
Практический метод расчета [9, 19, 39] изменения индекса приведенного уровня ударного шума ΔIу в результате устройства пола, предложенный автором, основан на экспериментальной зависимости этой величины от конструктивных параметров пола:

Величина Δу2 учитывает материал и конструкцию пола. При полах из досок или из паркета по дощатому основанию принимают Δу2=3 дБ; при полах из паркета, линолеума, релина, твердых древесноволокнистых плит, уложенных по монолитной стяжке или мелкоразмерным бетонным плитам основания пола, Δу2=0; при тех же покрытиях, уложенных по сборным крупноразмерным бетонным основаниям пола, Δу2=—ЗдБ.
Величина Δу3 учитывает влияние звукоизоляционной прослойки на демпфирование перекрытия. В случае применения засыпок из песка, шлака и т.д. принимают Δу3=1,5 дБ, в других случаях — Δу3=0.