Условия, принятые Рэлеем, привели к решению задачи о звукоизолирующей способности акустически однородного ограждения в форме так называемого закона массы
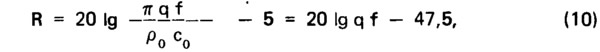
где q — поверхностная плотность плиты, кг/мг; f — частота звука, Гц; ρ0 — плотность воздуха, кг/м3 ; c0 — скорость звука в воздухе, м/с.
Согласно закону массы звукоизолирующая способность конструкции зависит только от ее поверхностной плотности, т.е. от массы единицы ее поверхности и от частоты звука. Влияние жесткости и демпфирования на звукоизолирующую способность конструкции не учитывается. Удвоение поверхностной плотности конструкции приводит к увеличению звукоизолирующей способности на всех частотах на 6 дБ.
Частотные характеристики конструкций различной поверхностной плотности представляют собой семейство параллельных прямых, имеющих темп роста звукоизолирующей способности 6 дБ на каждую октаву (увеличение звукоизолирующей способности на 6 дБ при удвоении частоты).
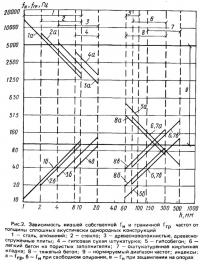
Измерения звукоизолирующей способности конструкций показывают, что их частотные характеристики существенно отличаются от таковых, построенных по закону массы. У реальных конструкций вместо равномерного увеличения звукоизолирующей способности во всем диапазоне при росте частоты звука наблюдаются участки с различным темпом ее роста, а также участки, на которых звукоизолирующая способность не увеличивается и даже снижается при повышении частоты звука. Эти отклонения от закона массы можно объяснить при рассмотрении волновых процессов в конструкции и в воздухе помещения с учетом явлений частотного и пространственного резонанса. Очертание частотной характеристики в нормируемом диапазоне определяется, в первую очередь, значениями характерных частот: низшей собственной частоты и граничной частоты волнового совпадения. От них зависит положение в нормируемом диапазоне специфических участков частотной характеристики, каждому из которых соответствует особый механизм прохождения звука и формирования звукоизолирующей способности конструкции. Конструкции из бетона и кирпичной кладки (в дальнейшем называемые массивными) и конструкции из тонких листовых материалов значительно отличаются друг от друга расположением граничной частоты волнового совпадения fгр относительно низшей собственной частоты fн конструкции и границ нормируемого диапазона (рис. 2). На графике отмечены границы применяемых на практике толщин материалов.
Низшая собственная частота конструкций из листовых материалов, применяемых обычно в сочетании с несущим каркасом, определена для пластины размером 1х0,5, массивных конструкций — для плиты размером 5х2,5 м.
Граничная частота тонких листовых конструкций находится либо за пределами нормируемого диапазона, либо в верхней его части (не ниже 1000 Гц). Низшая собственная частота расположена, как правило, за низшей границей нормируемого диапазона. Дистанция между низшей собственной и граничной частотами у конструкций из листовых материалов составляет от 4 до 10 октав.
Граничная частота массивных конструкций расположена в нижней части нормируемого диапазона (не выше 500 Гц) либо за его нижней границей. Наибольшая дистанция между низшей собственной и граничной частотами составляет около 4 октав. У конструкций толщиной 12 см и более она снижается до 1—2 октав, а у конструкций толщиной 20 см и более граничная частота может быть ниже, чем низшая собственная частота.
Указанные особенности в расположении характерных частот листовых и массивных конструкций определяют существенные различия в характере изменения их звукоизолирующей способности в нормируемом диапазоне частот.
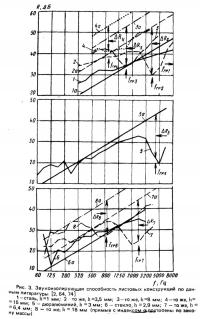
Фактические частотные характеристики листовых конструкций сильно отличаются от зависимостей, построенных по закону массы (рис. 3). Наиболее резкие отличия наблюдаются в области, расположенной вблизи граничной частоты конструкции fгр. Основной причиной существенного снижения звукоизоляции в этой области являются пространственно-частотные резонансы, увеличивающие амплитуду колебаний конструкции и тем самым передачу звуковой энергии из одного помещения в другое. Наибольшее снижение звукоизолирующей способности по сравнению с законом массы (на граничной частоте) ΔR зависит от плотности спектров собственных частот ограждения и помещения в этой области, определяющих вероятность реализации пространственно-частотных резонансов и их число в 1/3 октавной полосе, а также от демпфирования конструкции, определяющего высоту резонансных пиков. Плотность спектра собственных частот ограждения возрастает по мере удаления от низшей собственной частоты fн. Отношение fгр/fн хорошо характеризует плотность спектра собственных частот ограждения в области граничной частоты.
М.Хекль [69] и К.Гезеле [64] предложили определять снижение звукоизоляции на граничной частоте (по сравнению с вычислением ее по закону массы), пользуясь формулой
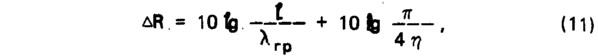
где l — длина пластины, не ограниченной в одном направлении; λгр — длина изгибной волны на граничной частоте; η — коэффициент потерь.
Для плиты, не ограниченной в одном направлении, l/λгр=0,5·√
Из рис. 3 видно, что по мере снижения fгр уменьшается и величина ΔR. При больших значениях fгр в частотной характеристике образуется "провал"; при значениях fгр<1000 Гц глубина "провала" становится незначительной, и участок частотной характеристики в окрестностях граничной частоты приближается к горизонтальной линии — "плато".
При малых размерах ячейки несущего каркаса листовой конструкции ее низшая резонансная частота приближается к нормируемому диапазону или даже входит в него. По данным В.Н. Бобылева [2], на частотах ниже fн звукоизолирующая способность конструкции на 15—35 дБ выше, чем по закону массы.
Таким образом, звукоизолирующая способность акустически однородных конструкций из листовых материалов в нормируемом диапазоне определяется положением граничной и низшей собственной частот, числом реализуемых частотных и пространственно-частотных резонансов и высотой возникающих резонансных пиков. В свою очередь указанные параметры зависят от соотношения поверхностной плотности и цилиндрической жесткости конструкции, ее демпфирования, условий закрепления по контуру и от размеров этой конструкции (в плане) и разделенных ею помещений. Лишь на достаточном удалении от fн и fгр (между ними) закон массы приближенно отражает фактическую звукоизолирующую способность ограждения. Уменьшение граничной частоты листовой конструкции, например, в результате увеличения ее жесткости при заданной поверхностной плотности приводит к уменьшению звукоизолирующей способности ограждения в нормируемом диапазоне частот.
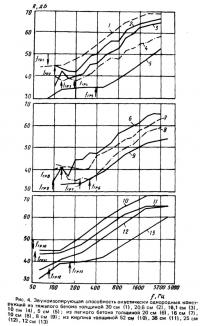
Частотные характеристики звукоизолирующей способности массивных конструкций (из тяжелого, легкого бетона1 и кирпичной кладки, оштукатуренной с двух сторон) имеют схожие очертания (рис. 4). В начале нормируемого диапазона располагается участок с примерно постоянной звукоизолирующей способностью, затем она довольно равномерно возрастает. Первый участок — это плато, образовавшееся вблизи граничной частоты. Теоретическое определение звукоизолирующей способности на граничной частоте затруднено. Для частот, превышающих fгр более чем на две октавы (f>4fгр), предложены следующие аналитические выражения звукоизолирующей способности акустически однородного ограждения:
Л. Кремером [60] на основе рассмотрения безграничной плиты
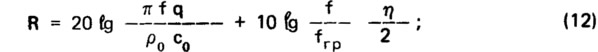
М. Хеклем [69] на основе рассмотрения плиты, ограниченной в одном направлении
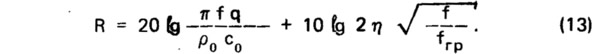
Первые члены правой части обеих формул выражают закон массы, вторые — учитывают расположение граничной частоты, которое определяется соотношением поверхностной плотности и жесткости плиты, и влияние коэффициента потерь материала. Формула (12) дает темп роста звукоизолирующей способности 9 дБ/окт, формула (13) — 7,5 дБ/окт. Уменьшение граничной частоты массивной конструкции, например в результате увеличения ее жесткости при заданной поверхностной плотности, приводит к увеличению звукоизолирующей способности ограждения в нормируемом диапазоне частот.
Ряд авторов предлагают определять звукоизолирующую способность в зоне граничной частоты, подставляя в формулу (12) f=fгр. Эта величина оказывается зависимой только от характеристик материала — плотности ρ, модуля упругости Е и коэффициента потерь η — и не зависит от толщины сплошной плиты:
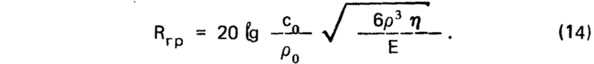
Такой вывод противоречит результатам эксперимента: с увеличением толщины плиты (с уменьшением fгр) звукоизолирующая способность ее в области граничной частоты возрастает (см. рис. 4). Это объясняется уменьшением плотности спектра собственных частот плиты по мере приближения fгр к fн и, следовательно, уменьшением числа реализуемых пространственно-частотных резонансов.
Теория М.С. Седова [45—47] позволяет получать результаты, более близкие к экспериментальным, однако она требует трудоемких вычислений, что несколько затрудняет ее практическое использование.
Трудности использования чисто теоретических методов послужили причиной появления практических методов расчета массивных акустически однородных конструкций. Первый из них предложен Б. Уоттерсом [81]. Им принято идеализированное очертание частотной характеристики звукоизолирующей способности в виде ломаной линии. В области, прилегающей к граничной частоте, расположен отрезок горизонтальной прямой — плато, до и после него — наклонные отрезки прямых. Расчетными параметрами, которые приняты на основе теоретических выводов и экспериментальных данных, являются ордината плато Rпп, его ширина, привязка плато к граничной частоте и уклоны наклонных участков (дБ/окт).
Б.Уоттерс предложил считать ординату и ширину плато постоянными для каждого материала, а уклоны прямых равными: до плато — 6 дБ/окт, после плато — 10 дБ/окт. Положение расчетной частотной характеристики в нормируемом диапазоне определяется граничной частотой, а форма ее остается неизменной для всех конструкций из данного материала.
При дальнейшем усовершенствовании описываемого метода [37, 50] величину Rпп стали считать зависимой от поверхностной плотности конструкции, что учитывает экспериментальные данные. При определении методом расчета [37, 50] индекс звукоизоляции зависит только от поверхностной плотности конструкции. Не учитывается влияние жесткости конструкции, связанное с использованием бетонов, характеризующихся различным соотношением плотности и модуля упругости, а также с применением элементов различных поперечных сечений. Из расчетов последним методом следует, что одинаковую звукоизоляцию имеют конструкции из тяжелого и легкого бетонов при равных поверхностных плотностях. Такой вывод не согласуется с экспериментальными данными (см. п.7).
В главе СНиП П-12-77 [54] приведен вариант рассматриваемого метода построения расчетной частотной характеристики, в котором величина Rпп принята зависимой от поверхностной плотности конструкции, а частота, определяющая положение горизонтального участка,— от ее толщины для четырех градаций плотности бетона. Этот вариант расчета частотной характеристики в определенной мере учитывает влияние на звукоизоляцию плотности бетона и формы сечения элемента. Однако он не позволяет учесть влияние изменения модуля упругости бетона при заданной плотности. В результате отсутствия ограничений формы сечения конструкций, для которых можно использовать расчет, создается опасность получения завышенных результатов, например для ребристых плит и плит с большими пустотами.
При проектировании жилых зданий расчетная частотная характеристика звукоизолирующей способности конструкции — только промежуточный этап для определения индекса звукоизоляции, поэтому для проектировщика важно иметь непосредственную зависимость индекса звукоизоляции от поверхностной плотности конструкции.
Для конструкций сплошного сечения из заданного материала можно получить зависимость Iв от q, близко совпадающую с экспериментальной. Подобная зависимость для конструкций сплошного сечения из тяжелого бетона, предложенная автором [9, 19, 39, 49, 54], выражена двумя формулами:
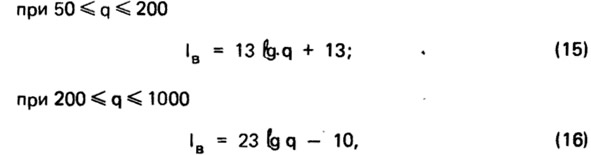
где q — поверхностная плотность конструкции, кг/м2.
Зависимости (15) и (16) можно использовать для расчета звукоизоляции акустически однородных конструкций из других видов бетонов и других поперечных сечений при условии учета влияния на звукоизоляцию характеристик материала и сечения.
Анализ экспериментальных данных показал, что звукоизоляция конструкций из тяжелого и легкого бетонов одинакова, если равны их граничные частоты. Это позволяет найти простое соотношение между поверхностными плотностями ограждений из тяжелого и легкого бетонов, обеспечивающих равную звукоизоляцию, приравняв выражения их граничных частот:
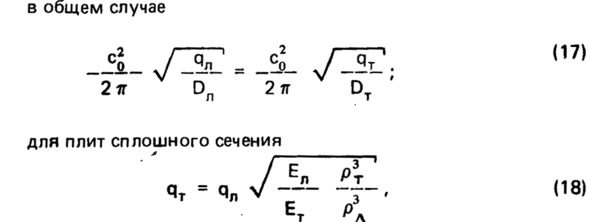
где величины с индексом "л" соответствуют конструкции из легкого бетона, а с индексом "т" — конструкции из тяжелого бетона.
Поверхностная плотность ограждения сплошного прямоугольного сечения из тяжелого бетона, имеющего одинаковую звукоизоляцию с рассматриваемой конструкцией из другого бетона или другого сечения, названа эквивалентной поверхностной плотностью q3 [19]:
где q — поверхностная плотность рассматриваемой конструкции; к — коэффициент, учитывающий параметры материала и поперечного сечения конструкции.
После подстановки в подкоренное выражение формулы (18) усредненных характеристик тяжелого бетона: Е=2,65·1010 Па и ρ=2400 кг/м3 получаем для конструкций сплошного сечения из легкого бетона
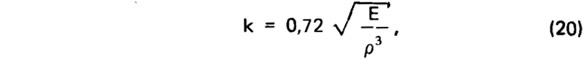
где Е — модуль упругости легкого бетона, Па; ρ — плотность легкого бетона, кг/м3.
Таким образом, индекс звукоизоляции Iв акустически однородных легкобетонных конструкций можно вычислить по формулам (15) или (16), подставляя в них величину q3, подсчитанную по формулам (19) и (20). Для определения индекса звукоизоляции 1в конструкций из кирпичной кладки может быть использована предложенная автором эмпирическая зависимость [9]:
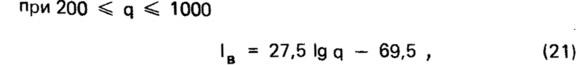
где q — поверхностная плотность конструкции, кг/м2.
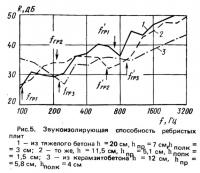
Акустически однородные конструкции могут иметь кроме сплошного ребристое или пустотное сечение. Согласно принятому определению ребристые плиты, строго говоря, не являются акустически однородными. Колебания полки ребристой плиты могут отличаться от колебаний плиты в целом. Это сказывается на звукоизолирующей способности ограждения. На рис. 5, где показаны частотные характеристики трех ребристых плит, измеренные на испытательном стенде ЦНИИЭП жилища [15], видны плато или провалы в двух областях. Первая соответствует граничной частоте плиты в целом fгр, вторая — граничной частоте полки fIгр. Решающее влияние на звукоизолирующую способность ребристой конструкции в нормируемом диапазоне частот оказывает наличие плато или провала в области граничной частоты полки fIгр, поэтому с достаточной точностью индекс звукоизоляции ребристой плиты можно определять как для сплошной плиты из того же материала толщиной, равной толщине полки по формуле (15) или (16).
Плиты с пустотами круглого сечения являются акустически однородными во всем нормируемом диапазоне частот.
На основе анализа экспериментальных данных были определены значения коэффициента к для подсчета эквивалентной поверхностной плотности плит с круглыми пустотами:
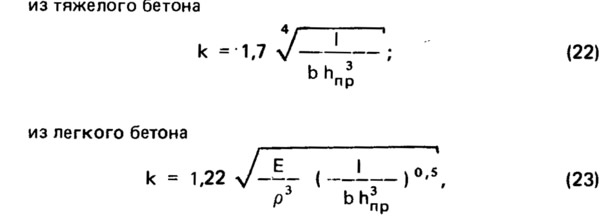
где Е — модуль упругости легкого бетона, Па; ρ — его плотность, кг/м3; I — момент инерции сечения плиты с круглыми пустотами; b — ширина сечения; hпр — приведенная толщина сечения плиты.
Эти же формулы можно использовать для расчета плит с пустотами не круглого сечения, которые удовлетворяют условие (5). В случаях, когда условие (5) не выполнено, например при пустотах овального сечения, вытянутого вдоль поверхности плиты, формулы (22) и (23) неприменимы. Самостоятельные колебания тонких стенок пустот, отличные от колебаний всей плиты, вызывают пространственно-частотные резонансы на высоких частотах, что снижает звукоизолирующую способность конструкции в нормируемом диапазоне.
В рассмотренных выражениях (15), (16) для определения индекса звукоизоляции конструкций из бетона отсутствует коэффициент потерь η, который стабилен для большинства видов бетона. Изменение коэффициента потерь бетона до 50% не приводит к заметному изменению коэффициента потерь ограждения, который в большей степени зависит от потерь звуковой энергии на его краях. Если приняты специальные меры для повышения коэффициента потерь конструкции по сравнению с величиной η0, характерной для ограждений из бетона, это легко учесть.
Из формул (11)—(13) видно, что изменение величины η приводит к одинаковому изменению звукоизолирующей способности конструкции в области, прилегающей к граничной частоте, и на более высоких частотах, т.е. во всем нормируемом диапазоне. Если конструкция имеет коэффициент потерь η>η0, это можно учесть, прибавив к расчетному индексу Iв поправку:
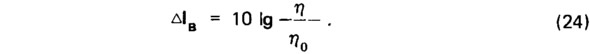
Возможны случаи, когда в акустически однородной конструкции использованы два материала с различными коэффициентами потерь, например, в бетонной конструкции с пустотами, заполненными сыпучим материалом — песком, шлаком, керамзитом и т.д. Коэффициент потерь этих сыпучих материалов примерно в 20 раз выше, чем у обычных бетонов. В подобных случаях результирующий коэффициент потерь конструкции зависит от взаимного расположения материалов, отношения их коэффициентов потерь, модулей упругости и поверхностных плотностей [77, 78]. Как показано ниже, экспериментально установлено, что при заполнении круглых пустот в бетонных плитах песком, шлаком, керамзитом или другим подобным материалом дополнительная звукоизолирующая способность, связанная с повышенным коэффициентом потерь сыпучего материала, может быть учтена поправкой ΔIв = 1,5 дБ к расчетному индексу Iв.
Примечания
1. Здесь и далее "легким бетоном" назван легкий бетон на пористых заполнителях и цементном вяжущем. Другие виды легких бетонов оговорены особо.