По СНиП коэффициент лобового сопротивления круглых цилиндров принимают по рис. 3.25, построенному для средней шероховатости цилиндров, например стальных дымовых труб, стальных трубопроводов, трубчатых элементов решетчатых стальных конструкций и т. п.
При вычислении числа Рейнольдса скорость потока определяют по формуле
где n — коэффициент перегрузки, равный 1,2 для всех видов сооружений, за исключением высоких сооружений с периодом колебания более 0,25 сек, для которых он принимается равным 1,3;
q — нормативный скоростной напор ветра для рассматриваемого района и высоты сооружения в кГ/м2;
m — коэффициент пульсации, принимаемый в зависимости от рассматриваемой высоты сооружения по табл. 2.3.
При определении ветровой нагрузки на конструкции, составленные из стержней круглого профиля, коэффициент лобового сопротивления берется с учетом шероховатости и числа Рейнольдса, вычисленного для каждого диаметра цилиндра.
В расчетах конструкций из круглых цилиндров (трубы, провода, канаты) за рубежом распространены равноценные числу Рейнольдса критерии; в частности, закризисным обтеканием считается, когда Vd≥7 или d√
Коэффициент лобового сопротивления шероховатых круглых цилиндров в зависимости от числа Рейнольдса показан на рис. 3.25. По нормам ГДР шероховатость гладких цилиндров строительных конструкций принимается равной 2·10—4, при умеренной шероховатости — 4·10—4, при шероховатой поверхности, например обледенелой, — 8·10—4. Размеры зерен шероховатости: для цельнотянутых и прокатных труб принимаются 0,01—0,05 мм, для сварных стальных труб — 0,05—0,2 мм, для стальных труб, образованных из листа с помощью заклепок или болтов, в зависимости от числа заклепок или болтов на единицу длины, — 0,2—2 мм. Шероховатость стальных трубчатых элементов решетчатых конструкций принимается 4·10—4. Эти данные относятся к трубам с нерегулярной шероховатостью.
Шероховатость может быть упорядоченной, например в виде регулярных ребер различной формы поперечного сечения по образующим цилиндрам, волнистый с разной длиной и высотой волны и др.
По французским нормам коэффициент лобового сопротивления бесконечно длинных многогранных призм без ребер и закруглений углов приведен в табл. 3.4.

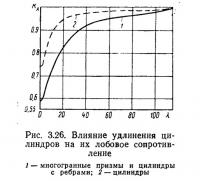
Коэффициент лобового сопротивления круглого цилиндра с ребрами или выступами высотой 0,01—0,1 диаметра цилиндра равен 1,16; шероховатого, но без ребер, при закризисном обтекании — сх=0,75. При конечной длине цилиндра коэффициент лобового сопротивления определяется умножением на коэффициент, значение которого принимают по рис. 3.26.
Коэффициент лобового сопротивления бесконечно длинного цилиндра с регулярными ребрами квадратного или треугольного сечения (шероховатость 0,04), волнистого с крупной, средней и мелкой волной соответственно с шероховатостью 0,033; 0,03 и 0,01 равен 0,65—0,75. Наибольшие значения коэффициента сх у цилиндра с треугольным гофром (0,75) и мелковолнистым (0,70). Эти данные относятся к закризисному обтеканию цилиндров— числа Рейнольдса 0,4·106÷1,8·108. Коэффициент лобового сопротивления гладкого круглого цилиндра, определенный в той же аэродинамической трубе и в том же интервале чисел Рейнольдса, — 0,4—0,55.
Исследование сопротивления моделей газгольдеров с ребрами (относительная шероховатость 0,006) при отношении высоты к диаметру, равном двум (удлинение λ=4), и числе Рейнольдса Re=6,3·105 и более показало, что коэффициент cx=0,68; коэффициент лобового сопротивления гладкого цилиндра того же удлинения в нижекритической области равен 0,74 (Флаксбарт).
Коэффициент лобового сопротивления изолированного круглого цилиндра, наклоненного к потоку под углом скольжения β, понижается с ростом этого угла быстрее, чем коэффициент сх плоской пластинки. Картина похожа на обтекание потоком как бы эллиптического цилиндра. Опытные значения коэффициента лобового сопротивления цилиндра хорошо аппроксимируются графиком sin3β. По другим данным, показатель степени ближе к 2,7. Коэффициент полного сопротивления цилиндра, расположенного под углом β к скорости потока, равен: cn=cxsin2β [15].
Для определения лобового сопротивления цилиндров с учетом числа Рейнольдса скорость потока принимают умноженной на sin α или sin β, если цилиндр расположен под углами атаки а или скольжения β. В случае обтекания цилиндра до кризиса такое уточнение не влияет на его сопротивление в большом интервале чисел Рейнольдса (см. рис. 3.8).
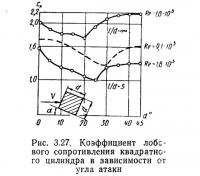
Коэффициенты лобового сопротивления квадратного и шестигранного цилиндров бесконечной длины при Re=(0,34÷1,8)·108 и направлении потока на грань — 1,08 и 0,93, при потоке на угол — 1,18 и 1,23 соответственно.
На рис. 3.27 приведены опытные значения коэффициента лобового сопротивления квадратного цилиндра (призмы) бесконечной длины и с удлинением λ=5 в зависимости от угла атаки. Число Рейнольдса в опытах было равно 1,8·105. Как видно на рис. 3.27, у длинного цилиндра минимум значения коэффициента сх наступает при угле атаки α=20°, а у цилиндра с удлинением λ=5 — при угле λ=25°. Характерно, что наибольшая нагрузка на квадратную сплошностенчатую башню будет при действии ветра по диагонали (α=45°), так как ее наветренная площадь возросла в 1,41 раза, а значение сх снизилось лишь в 1,3 раза. Коэффициент лобового сопротивления цилиндров треугольного и полукруглого сечений (λ=8; Re=90000) изменяется при противоположных направлениях потока приблизительно в два раза.
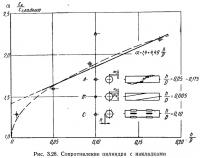
На рис. 3.28 приведены данные исследований в трубе круглых цилиндров (Re=565000) с различно расположенными пластинчатыми накладками — интерцепторами, используемыми для гашения вибрации трубчатых конструкций при ветре [16]. Коэффициент лобового сопротивления цилиндра с накладками увеличивается до двух и более даже при относительно невысоких полосах. Цилиндры с накладками приближаются к многогранным призмам, коэффициент лобового сопротивления которых может быть до 1,4. Эти данные свидетельствуют о недопустимости простого суммирования ветровой нагрузки на гладкий круглый цилиндр с нагрузкой на небольшие по размерам детали. Коэффициент сх цилиндра с деталями на нем должен приниматься повышенным.
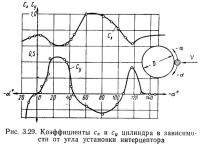
Влияние небольшого изменения формы поперечного сечения тела на коэффициент лобового сопротивления показано также на круглом цилиндре с невысокой накладкой, установленной по образующей под различными углами к передней критической точке (рис. 3.29). Накладкой служила круглая проволока диаметром 3 мм. Опыты проводились на цилиндре диаметром 30 мм с удлинением 4,4; число Рейнольдса до 5,5·104. Как видно, накладка может как повышать, так и понижать лобовое сопротивление цилиндра. Наибольшее значение коэффициента сх=1,02 цилиндра с накладкой будет при α=60÷70°, наименьшее сх=0,6 — при α=20÷30°. Существенно то, что появилась стационарная подъемная сила, величина и знак которой зависят от места накладки на цилиндре (МГУ).
Наибольший коэффициент лобового сопротивления получается при накладках, расположенных по образующим цилиндра; у цилиндра с геликоидальными накладками он меньше. Наименьший коэффициент сопротивления будет в случае спирально расположенных накладок, так как на шаге спирали будут участки, где интерцептор уменьшает лобовое сопротивление цилиндра (см. рис. 3.29).
В нормах ГДР для расчета железобетонных труб, применяемых в качестве опор телевизионных антенн, местное продольное утолщение по образующей цилиндра учитывают в величине коэффициента сх. При расположении утолщения против потока (угол α=0°) значение сх принимают 0,85, при угле α=90° берут cx=1,15, при угле α=180° cx=0,6. Коэффициент лобового сопротивления трубчатой железобетонной башни с окнами по этим нормам принимается равным 0,7.
Коэффициенты лобового сопротивления проводов и стальных канатов спиральной (одинарной) свивки в зависимости от произведения Vd приведены на рис. 3.30 (ВНИИЭ). Разброс опытных величин коэффициента (заштрихованная область) находится в пределах 0,9—1,25. Причина его — влияние величины диаметра провода, количества проволок и диаметра их в верхнем повиве.
Для канатов двойной свивки, т. е. образованных несколькими прядями, свитыми из проволок, коэффициент лобового сопротивления принимают до кризиса равным 1,3 и 1,2 — после кризиса; для проводов и канатов закрытого типа, т. е. из профилированной проволоки во внешнем повиве, коэффициент cx=1,1 и 0,3 соответственно. Коэффициент лобового сопротивления кабелей вантовых и висячих мостов зависит от конструкции кабеля: при шестигранном или другом сечении каната принимают коэффициенты сх для многогранных призм (см. например, табл. 3.3 или 3.4). Крепежные детали на кабелях учитывают конструктивным коэффициентом или коэффициент лобового сопротивления деталей принимают равным 1,2.
По нормативным материалам для линий электропередачи при направлении ветра под углом к хорде (оси) нити поперечную нагрузку на нее принимают пропорциональной синусу угла между ветром и хордой.
Нагрузка на оттяжки-ванты складывается из собственного веса каната, льда на нем и давления ветра, принимаемого пропорционально sin β.
Тогда
где g — погонный вес каната в кГ/м;
β — угол оттяжки с горизонтом;
w — нагрузка от ветра на единицу длины каната, хорда которого нормальна к направлению потока, в кГ/м;
φ — угол между направлением оттяжки в плане и началом отсчета;
θ — угол между скоростью ветра и началом отсчета, принимаемым за направление наветренной оттяжки.
Горизонтальная узловая нагрузка на ствол мачты с оттяжками при действии ветра на несколько одинаковых оттяжек одного яруса, расположенных равномерно по окружности и под одинаковым углом к горизонту,
где n — число оттяжек в узле;
l — длина хорды оттяжки;
β — угол между хордой оттяжки и горизонтом.
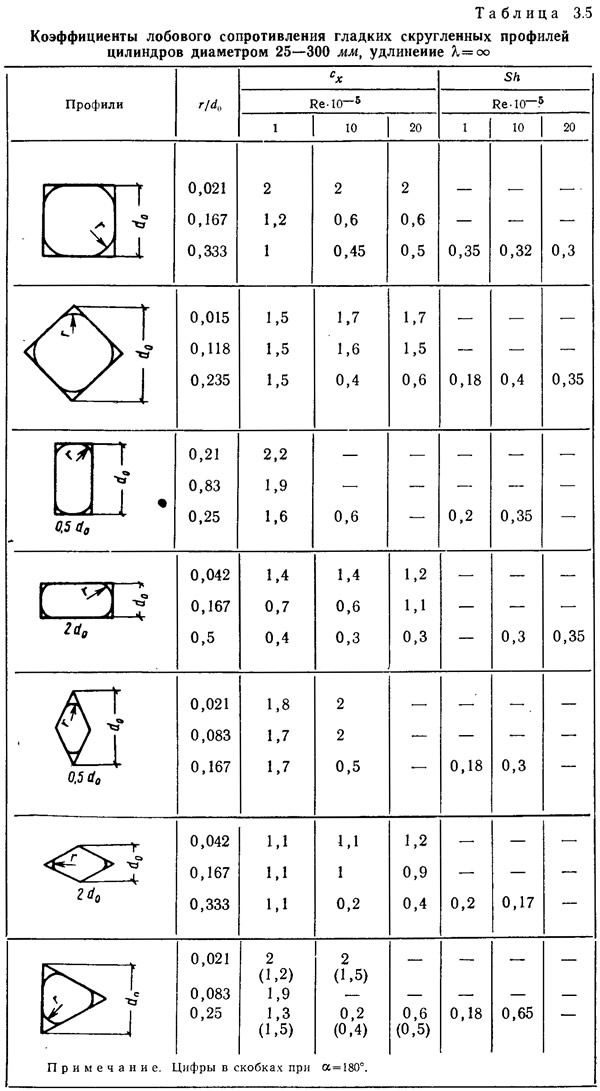
В ряде случаев нужны данные о сопротивлении цилиндров разнообразных профилей с различным радиусом скругления острых краев [17]. В табл. 3.5 приведены основные сведения о цилиндрах бесконечной длины. Общим для всех профилей с относительно большими радиусами скругления краев является наступление кризиса обтекания, характеризуемое, как и у круглого цилиндра, резким снижением коэффициента лобового сопротивления. При малом радиусе закругления цилиндры ведут себя как профили с острыми краями, при большом — у них наступает кризис в области чисел Рейнольдса, близких к критическим числам Рейнольдса круглого цилиндра. Разброс чисел Струхаля в области кризиса значительно больше, чем у круглого цилиндра, например, у треугольного сечения цилиндра — с 0,18 до 0,65. С увеличением радиуса скругления краев цилиндров их коэффициент лобового сопротивления до кризиса не изменяется или понижается, но не столь заметно. У профилей с большим относительно характерного размера радиусом закругления коэффициент сх при кризисе падает очень сильно; например, у треугольного цилиндра после скругления с 1,3 до 0,2.
Поведение бесконечно длинного эллиптического цилиндра (отношение 1:2) в потоке зависит от ориентации его; если большая ось расположена поперек потока, то его коэффициент лобового сопротивления при числах Рейнольдса 104—5·105 остается неизменным и равным 1,7. С дальнейшим увеличением Re наблюдается небольшое падение коэффициента сх. При расположении цилиндра большой осью по потоку его коэффициент лобового сопротивления, равный 0,6 при Re=104, медленно растет и достигает 0,7 при Re=,1·105. Затем наступает кризис, при Re=7·105 коэффициент сх цилиндра становится минимальным и равным 0,1 для характерного размера 0,1 м и 0,14 — для размера 0,3 м. Кризис обтекания у такого цилиндра наступает раньше, что можно объяснить, по-видимому, большей величиной относительной шероховатости поверхности. При Re=2·108 коэффициент сх=0,6. Числа Струхаля, мало зависящие от числа Рейнольдса, равны: для эллиптического цилиндра большой осью по потоку Sh=0,13, поперек потока Sh=0,18÷0,2 (НАСА).
Коэффициент лобового сопротивления скругленных цилиндров конечной длины снижается, как и коэффициент сопротивления круглого цилиндра: он резко падает с уменьшением удлинения, начиная с λ=10 (см. рис. 3.4). При углах скольжения β≠0° лобовое сопротивление таких цилиндров с ростом этого угла снижается не так сильно, как круглого цилиндра. Коэффициент лобового сопротивления немного скругленных цилиндров при углах β≠0° следует скорее закону сопротивления плоской пластинки. Для учета в расчетах удлинения таких цилиндров можно воспользоваться данными на рис. 3.4 или рис. 3.26.