При анализе колебаний зданий и сооружений с присоединенными гасителями в качестве динамической модели сооружения используют, как правило, систему с одной степенью свободы. Как указано в [90], такой моделью можно пользоваться, если при изменении собственных частот сооружения в 1,5-2 раза резонансные явления возможны лишь для одной собственной частоты сооружения. Для подавляющего большинства зданий, возводимых в сейсмических районах, это условие выполняется.
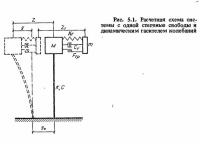
Рассмотрим колебания системы (рис. 5.1), полагая, что основание движется по закону y0(t) . На рисунке обозначено: М — главная (приведенная) масса защищаемого объекта; m — масса гасителя; k, kг - жесткости основной системы и упругого элемента гасителя; с, сг - коэффициенты вязкого сопротивления для главной массы и гасителя; Fтр - сила сухого трения в гасителе; z, zг - перемещения главной массы и гасителя относительно неподвижной системы отсчета. Дифференциальные уравнения движения главной массы и гасителя могут быть представлены в следующем виде:
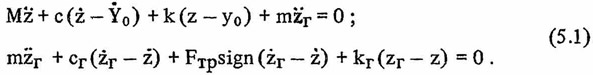
Во второе уравнение системы (5.1) входит сила кулонова трения, так как в некоторых конструкциях динамического гасителя колебаний демпфирование в гасителе создается введением элементов сухого трения.
Система уравнений (5.1) может быть преобразована следующим образом:
где y - смещение главной массы относительно основания; u - смещение массы гасителя относительно главной массы.
Введем обозначения: ω = (k/М)1/2; fг = (kг/m)1/2 — парциальные частоты; ξ = с/2Мω; λ = cг/2mfг — безразмерные параметры вязкости для главной массы и гасителя; v = m/M - относительная масса гасителя.
Используя данные обозначения, преобразуем систему (5.2) в следующую:
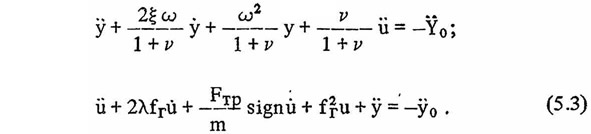
Поскольку член, выражающий затухание от силы сухого трения во втором уравнении системы (5.3), является нелинейным, то точное решение данной системы уравнений возможно только численным методом. В случае необходимости однократного расчета решение системы (5.3) численным методом не представляет особых трудностей, но при проведении многократных оптимизационных расчетов для различных параметров основной системы и параметров гасителя использование численного метода решения становится нерациональным.
Воспользуемся приближенным подходом, в основу которого положим представление движения массы гасителя по синусоидальному закону. Это можно сделать, исходя из следующего соображения. В режиме, близком к резонансу системы, амплитуда колебаний массы гасителя становится большой. Известно, что влияние силы сухого трения на колебание массы уменьшается с увеличением ее амплитуды колебания и при больших амплитудах форма колебания массы гасителя приближается к синусоидальной.
Заменим нелинейный член во втором уравнении системы (5.2) эквивалентным членом с коэффициентом в, определяемым по следующей формуле:
где р0 - частота колебаний основания.
Тогда система (5.3) может быть записана в следующем виде:
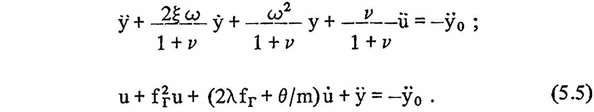
Дифференциальные уравнения (5.3) и (5.5) являются исходными для точного или приближенного анализа колебаний системы с динамическим гасителем колебаний при различных законах движения основания.
Движение основания по гармоническому закону
Рассмотрим колебания системы (рис. 5.1), вызванные движением основания по закону
Колебания системы описываются уравнениями (5.5), решение которых ищем в виде
После подстановки (5.6) и (5.7) в (5.5) и некоторых преобразований имеем:
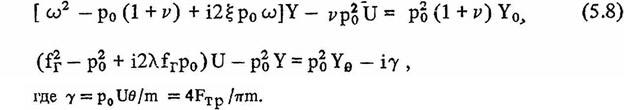
Введем обозначения: p = p0/ω — относительная частота воздействия; f = fг/ω — настройка гасителя; γ* = γ/Y0 — безразмерный параметр, характеризующий соотношение силы сухого трения в гасителе и инерционной силы массы гасителя, определяемой как произведение амплитуды ускорения основания и массы гасителя.
Используя данные обозначения, решение системы (5.8) представим в следующем виде:
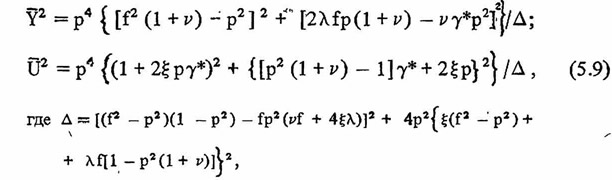
где
Таким образом, относительные смещения
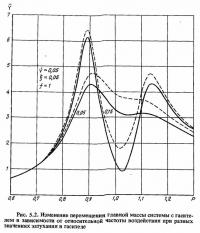
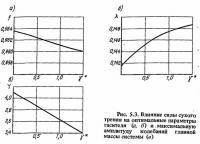
Значения обоих максимумов, имеющих место на рис. 5.2, зависят от параметров гасителя. Обычно масса гасителя и величина сухого трения в гасителе принимаются постоянными, а для достижения наибольшего эффекта гашения колебаний в основной системе варьируют настройкой и вязким затуханием в гасителе. На рис. 5.3 приведены графики зависимости значений оптимальных параметров гасителя и его максимальной амплитуды колебаний главной массы системы в зависимости от параметра γ*, полученные в результате численного анализа формулы (5.9). С увеличением γ* эффективность применения гасителя вырастает, но это положение действительно не при всех значениях γ*, так как при значениях γ*, больших, чем 2/πξ, сила сухого трения в гасителе будет превосходить силу инерции движения массы гасителя, и последний будет колебаться совместно с главной массой системы как одно целое. Таким образом, пользоваться формулами (5.9) и графиками на рис. 5.3 можно только в случае, когда γ* значительно меньше 2/πξ (в три и более раз).
В случае если γ* стремится к нулю, значения оптимальных параметров гасителя и максимальная амплитуда главной массы системы становятся независимыми от амплитуды воздействия и соответствуют значениям системы с гасителем, имеющим только вязкое затухание.
Движение основания по закону затухающих синусоид
В качестве упрощенного закона сейсмического движения грунта может быть принята одна затухающая синусоида или сумма нескольких затухающих синусоид, частота которых может иметь различные значения. Примем следующий закон изменения ускорения движения грунта:
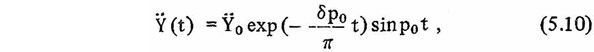
где δ - логарифмический декремент колебаний грунта.
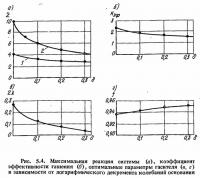
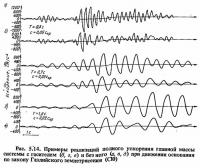
Дифференциальные уравнения колебаний системы с гасителем (5.3) при Fтр = 0 и с правой частью по формуле (5.10) решались на аналоговой вычислительной машине (АВМ) при ряде значений 5 [47]. В процессе решения проводилась оптимизация параметров гасителя. На рис. 5.4 приведены графики, полученные в результате оптимизации из условия минимума полного ускорения главной массы. По горизонтали на графиках отложена величина логарифмического декремента колебаний основания, а по вертикали на рис. 5.4, а отложены максимальные значения амплитуды полного ускорения главной массы системы с гасителем
На рис. 5.4, в и 5.4, г показаны графики изменения оптимальных параметров гасителя. Как видно из графиков, при возрастании декремента колебания основания оптимальное затухание гасителя заметно уменьшается, а оптимальная настройка изменяется незначительно.
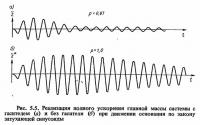
На рис. 5.5, а представлена реализация решения для системы с гасителем при одном из значений частоты воздействия, соответствующих максимальным значениям
Необходимо отметить, что реакция системы с гасителем чувствительна к отклонению параметров гасителя от оптимальных значений.
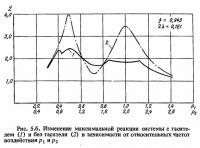
Рассмотрим работу системы с гасителем при движении основания по закону суммы двух затухающих синусоид. Положим, что сдвиг фаз между синусоидами равен нулю, соотношение частот двух затухающих синусоид p01 и p02 равно двум, а логарифмические декременты колебаний имеют одинаковую величину, равную 0,1. На рис. 5.6 приведены графики изменения 2* и Z системы, имеющей параметры гасителя: v = 0,05; f = 0,943 и 2λ = 0,121 (оптимальные при воздействии одной затухающей синусоиды).
Наличие второй затухающей синусоиды в основании приводит к снижению реакции как системы без гасителя, так и системы с гасителем. Для системы с одной степенью свободы получаются два максимума при p1 = 0,49 (р2 = 0,98) и р1 = 1,0 (p2 = 2,0), а для системы с гасителем четыре максимума. По характеру графика видно, что параметры гасителя стали неоптимальными, а коэффициент эффективности гашения снизился с 1,83 до 1,61.
Необходимо отметить, что добавление к основной затухающей синусоиде более высокочастотной синусоиды не приводит к значительному снижению Кэф, в данном случае он равен 1,71. Снижение Кэф до значения 1,61 происходит в случае, когда вторая синусоида имеет частоту более низкую, чем основная.
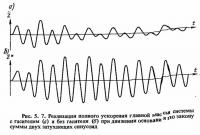
На рис. 5.7 приведены реализации полного ускорения главной массы системы с гасителем и без него при р1 = 0,49 и p2 = 0,98.
Движение основания, описываемое случайным процессом
Как уже ранее отмечалось, наиболее широко применяемыми моделями сейсмического движения грунта являются модели, основанные на представлении сейсмического воздействия случайным процессом.
Рассмотрим колебания системы с гасителем, описываемые системой уравнений (5.3) при Fтр = 0, полагая, что движение основания можно представить стационарным случайным процессом, имеющим спектральную плотность S0(р).
Дисперсия перемещений главной массы может быть определена по формуле
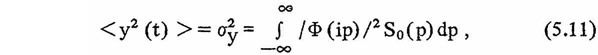
где Ф(ip) - передаточная функция системы с гасителем, определяющая комплексную амплитуду установившейся реакции системы на единичное воздействие e1ωt.
Передаточная функция может быть записана в следующем виде:
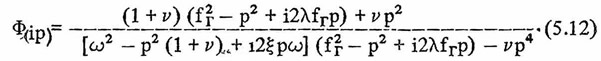
Для ряда функций S0(р) интеграл в формуле (5.11) с учетом (5.12) может быть вычислен в аналитической форме. Допустим, что ускорение движения основания представляет собой процесс типа белый шум. Тогда S0(р) = S0 = const и с помощью теории вычетов получим:
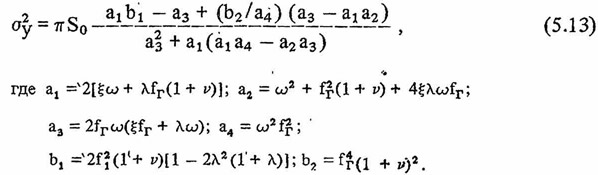
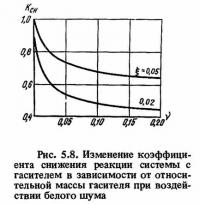
На рис. 5.8 приведены графики коэффициента снижения стандарта перемещений главной массы системы с гасителем по сравнению с соответствующим стандартом в системе без гасителя в зависимости от относительной массы гасителя. Значения стандарта вычислены по (5.13) при оптимальных параметрах гасителя, которые можно определить по следующим формулам:
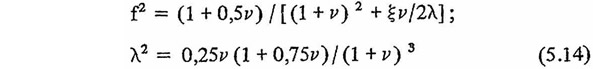
Необходимо отметить, что с точки зрения эффективности гасителя колебания белый шум является самым невыгодным из класса стационарных случайных воздействий. Белый шум в определенном диапазоне частот достаточно хорошо аппроксимирует процесс сильного землетрясения в эпицентральной зоне. При удалении от эпицентра спектр ускорений колебания грунта становится более узкополосным.
Наиболее часто сейсмические ускорения грунта в этом случае описываются случайным процессом, нормированная корреляционная функция и спектральная плотность которого соответственно равны:
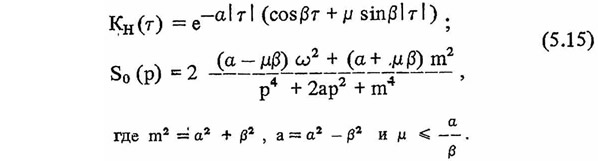
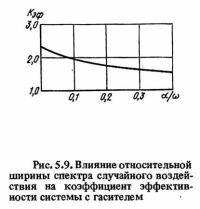
На рис. 5.9 приведен график коэффициента Кэф для системы, имеющей относительную массу гасителя 0,05, в зависимости от параметра а/ω, характеризующего относительную ширину спектра воздействия. Из графика следует, что эффективность применения гасителя возрастает с уменьшением ширины спектра воздействия.
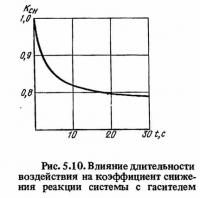
Известно, что длительность основной фазы землетрясения составляет от 10 до 40 с [58]. Представляет интерес оценить эффективность гасителя в зависимости от длительности землетрясения. На рис. 5.10 приведена зависимость коэффициента снижения ускорения Ксн, определяемого как отношение максимального ускорения главной массы системы с гасителем к максимальному ускорению системы без гасителя в зависимости от длительности воздействия белого шума. С увеличением длительности воздействия белого шума на систему эффективность гасителя увеличивается. При t > 10 с эффективность гасителя мало зависит.от длительности воздействия и величина коэффициента Ксн может считаться постоянной. Зависимость на рис. 5.10 получена по результатам расчетов на АВМ, при которых кратковременный случайный процесс моделировался с помощью генератора ГШ-1 [72]. Параметры системы были приняты следующие: парциальная частота главной массы 10 рад/с, затухание в основной системе 5% критического, относительная масса гасителя 0,05 и затухание в гасителе 11% критического. Значение настройки гасителя варьировалось от 0,91 до 0,99.
В процессе моделирования на выходе АВМ были получены реализации полного ускорения для системы с гасителем W(t) и системы без гасителя W(t)* при длительности процесса 5, 10, 20 и 30 с. Для каждой i-й реализации имеется свое значение Wi = max |Wi(t)|, которое было нормировано относительно среднеквадратичного значения ускорения основания. По полученным реализациям для каждого значения настройки гасителя построены гистограммы распределения нормированного максимального ускорения главной массы системы с гасителем, а также гистограммы распределения коэффициента снижения ускорения Ксн. Гистограмма распределения коэффициента Ксн при оптимальной настройке близка к симметричной и может быть аппроксимирована нормальным распределением. Из теоретической функции распределения, построенной по оценкам эмпирического распределения для записей длительностью 30 с, получено, что коэффициент Ксн изменяется с вероятностью 0,95 в пределах 0,56-1,03.
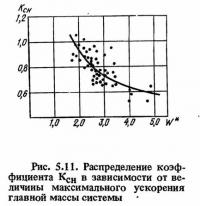
Таким образом, в некоторых случаях максимальное ускорение может снижаться почти в два раза, а в других может незначительно увеличиваться. Однако, как показывает анализ записей, увеличение ускорения главной массы системы с гасителем возможно только при малых по абсолютной величине максимальных ускорениях главной массы (рис. 5.11).
Функции распределения максимальных значений ускорения для системы с гасителем и без гасителя хорошо описываются двойным показательным законом, используемым в теории распределения крайних членов выборки:
ще а > 0 и q - параметры распределения.
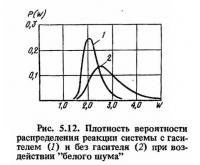
Оценки параметров распределения были вычислены с помощью процедуры Гумбеля [10]. Подставив вычисленные оценки распределений ускорений в формулу для плотности вероятности распределения р{W},которая записывается в следующем виде:
можно построить графики изменения плотностей вероятности этих распределений (рис. 5.12). Как видно из рис. 5.12, применение гасителя приводит не только к уменьшению среднего значения максимального ускорения, но и значительно уменьшает разброс вокруг этого среднего.
Используя функции распределения (5.16), можно определить коэффициент Ксн в зависимости от полного ускорения в системе без гасителя по следующей формуле:
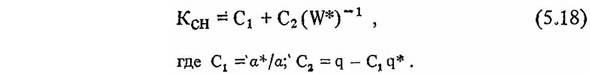
На рис. 5.11 приведен график изменения коэффициента Ксн в зависимости от ускорения W*, построенный по (5.18).
По полученным оценкам параметров распределений можно оценить степень повышения надежности конструкции при применении гасителя колебаний. Примем за условный критерий разрушения системы достижение полного ускорения главной массы уровня А. Тогда вероятность разрушения системы можно определить по следующей формуле:
Допустим, что система без гасителя при землетрясении разрушится с вероятностью, равной 0,5, тогда вероятность разрушения системы с гасителем при параметрах гасителя, близких к оптимальным, будет в пять раз меньше при ξ = 0,05 и в 20 раз меньше при ξ =0,02, что показывает на сильное влияние затухания в основной системе на оценку степени повышения надежности сооружения от установки гасителя колебаний.
Кроме анализа колебаний системы с одной степенью свободы и гасителем колебаний при воздействии кратковременного белого шума исследовалось влияние гасителя на колебания системы с двумя степенями свободы. На АВМ была смоделирована система с двумя степенями свободы, имеющая одинаковые массы и постоянную по высоте сдвиговую жесткость, при этом соотношение собственных частот системы составило 2,62. Величина первого периода собственных колебаний системы принята такой же, как и для системы с одной степенью свободы, рассмотренной выше.
К верхней массе системы был присоединен гаситель колебаний, настроенный на первую частоту собственных колебаний системы. Масса гасителя была принята равной 5 % приведенной массы системы с двумя степенями свободы, что составило 6,9 % верхней массы системы. Параметры гасителя были приняты такими же, как и для системы с одной степенью свободы.
Была рассмотрена также система с двумя гасителями колебаний. Кроме гасителя, настроенного на первую частоту собственных колебаний, к нижней массе системы присоединен гаситель, настроенный на вторую частоту собственных колебаний основной системы. Параметры второго гасителя были приняты такими же, как и для первого гасителя.
На вход системы с гасителями и без них подавался белый шум. На выходе записывались полные ускорения и относительные перемещения масс системы. По записям были построены гистограммы распределения нормированных максимальных ускорений и относительных смещений обеих масс системы. Максимальные за реализацию относительные смещения масс нормированы относительно статических перемещений первой и второй массы под действием условных поперечных сил, численно равных силам инерции переносного движения первой и второй массы системы.
Эмпирические распределения максимальных ускорений и относительных смещений масс системы с двумя степенями свободы с гасителем и без него могут быть описаны двойным показательным законом (5.16), как и в случае системы с одной степенью свободы. В табл. 5.1 приведены значения исследуемых функций Х(Р), вычисленных с вероятностью, не меньшей, чем 0,5 и 0,995, а также значения коэффициента снижения исследуемых функций Ксн(р). Из таблицы видно; что в статистическом смысле применение гасителя, настроенного на первую частоту собственных колебаний рассмотренной системы с двумя степенями свободы, приводит к снижению ускорения верхней массы на 18%, а ускорения нижней массы на 9 %. При этом снижение относительных смещений верхней и нижней масс практически одинаково и составляет 19%.

В системе с одной степенью свободы применение гасителя с такими же параметрами приводило к снижению ускорения масс на 20% и относительного смещения на 19%. С увеличением вероятности, с которой вычисляется коэффициент Ксн(Р) для системы с двумя степенями свободы, величина его уменьшается, хотя и в меньшей степени, чем в случае системы с одной степенью свободы.
На рис. 5.13 приведены графики изменения значений коэффициента снижения реакции масс системы, вычисленных по отношению медиан соответствующих гистограмм распределений, в зависимости от числа гасителей. Из графиков видно, что суммарное снижение ускорения верхней и нижней масс системы от установки обоих гасителей составило 25 и 32%, а снижение относительного смещения 21% для верхней массы и 23% для нижней массы.
Движение основания при реальных землетрясениях
Для анализа колебаний системы с гасителем с использованием акселерограмм реальных землетрясений [71, 73] в качестве расчетных были использованы записи Газлийского землетрясения, происшедшего 17 мая 1976 г. (компонента север-юг) и Карпатского землетрясения, происшедшего 4 марта 1977 г. (компонента север-юг). Эти два землетрясения могут рассматриваться как модели типичных землетрясений с близким и удаленным эпицентрами, и поэтому результаты расчета на записи этих землетрясений отражают диапазон эффективности гасителей при землетрясениях.
Параметры гасителя были приняты следующими: относительная масса 0,05, затухание 11% критического и настройка 0,96.
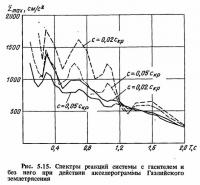
В результате решения (5.3) с помощью АВМ, на вход которой подавалось напряжение, изменявшееся по закону, соответствующему акселерограмме Газлийского землетрясения, были получены записи реакций системы с гасителем и без него при различных значениях периода собственных колебаний системы Т. Затухание в основной системе принималось 5 и 2% критического. На рис. 5.14 приведены примеры таких записей. По этим записям построены спектры максимальных ускорений главной массы системы с гасителем и без него для обоих значений затухания в основной системе.
Сравнение спектров для системы с гасителем (сплошная линия) и без него (пунктирная линия) (рис. 5.3.5) показывает, что введение гасителя в систему приводит к снижению ее сейсмической реакции практически при всех периодах Т, причем это снижение особенно существенно при периодах, соответствующих пиковым участкам спектров системы без гасителя. Значительно меньшая эффективность гасителей отмечается при периодах, соответствующих минимальным значениям ординат спектра. Такая особенность работы гасителя приводит к некоторому сглаживанию спектров за счет срезки их пиковых участков.
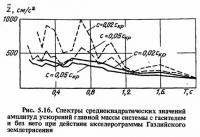
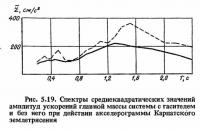
Спектры реакций относятся к числу основных исходных данных для расчета сейсмостойкости сооружений. Однако они дают информацию только о максимальных величинах реакций и не дают сведений о поведении сооружения в течение всего землетрясения. Одной из интегральных характеристик, которые позволяют судить об уровне колебаний сооружения во время всего землетрясения, является среднеквадратичное значение амплитуд реакции сооружения. Спектры таких значений z приведены на рис. 5.16.
Для Карпатского землетрясения эффективность гасителя оказалась несколько ниже, чем для Газлийского, хотя общие закономерности влияния гасителя на реакцию системы сохраняются. Снижение эффективности гасителя можно объяснить тем, что запись Карпатского землетрясения имеет в самом начале ускорения с амплитудой, сильно превышающей последующие. Поэтому реакция сооружения достигает своего максимального значения в начальной стадии землетрясения, когда гаситель еще не успевает сильно раскачаться. В связи с этим степень снижения амплитуд в начальной стадии землетрясения будет меньше, чем в последующей.
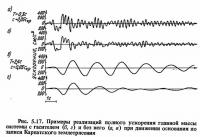
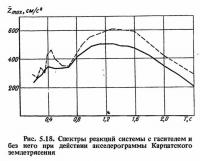
На рис. 5.17 приведены реализации полного ускорения массы системы с гасителем и без него при двух значениях Т и движении основания по записи Карпатского землетрясения, а на рис. 5.18 и 5.19 - соответствующие спектры реакций.
Оценка эффективности гасителя по расчету для систем со значениями периодов собственных колебаний, изменяющихся в широком диапазоне целесообразна только в том случае, если не имеется никакой информации о спектрах возможных землетрясений в данном районе. Если такая информация имеется, то не следует применять гасители для зданий с основным периодом собственных колебаний, попадающим в зону спектра с малой реакцией. В таком случае эффективность гасителя будет мала или полностью отсутствовать.
Таким образом, пользуясь имеющейся информацией о возможных спектрах будущих землетрясений и условной классификацией сооружений [20], для районов, где возможны такие землетрясения, как Газлийское, более рационально применять гасители для сооружений с периодом собственных колебаний менее, чем 1,1 с, а для районов., где возможны землетрясения типа Карпатского, наоборот, — для сооружений, имеющих период собственных колебаний более 1,1 с. При таком подходе к вопросу о целесообразности применения гасителя его эффективность возрастает.
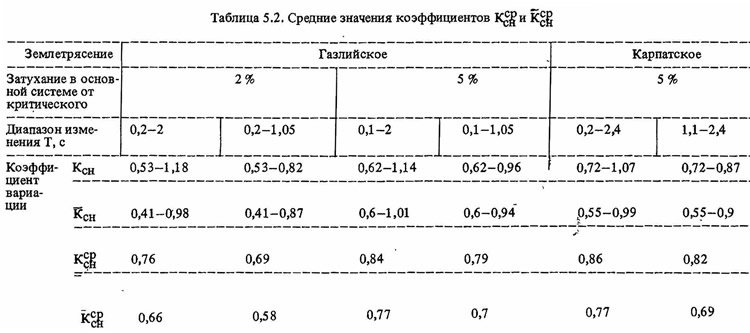
В табл. 5.2 приведены средние значения коэффициентов Kсрсн и
Из табл. 5.2 видно, что несмотря на то; что использованные для оценки эффективности гасителя записи землетрясений имеют существенно разный спектральный состав, средние значения коэффициентов снижения реакции практически одинаковы.
Для нескольких систем с двумя и тремя степенями свободы был выполнен анализ колебаний с использованием в качестве воздействия указанной выше записи Газлийского землетрясения. Этот анализ показал, что эффективность гасителя, настроенного на первую частоту собственных колебаний системы с несколькими степенями свободы, имеющей параметры, соответствующие обычным гражданским зданиям средней высоты, мало отличаются от эффективности гасителя, получаемой при расчете системы с одной степенью свободы.
Некоторое падение эффективности гасителя по снижению усилий в конструкциях возможно для верхней части сооружений. Для указанных выше зданий гасители, настроенные на вторую частоту собственных колебаний сооружения, устанавливать нецелесообразно, так как динамическая реакция уменьшается незначительно по сравнению с системой без гасителя.
В качестве примера рассмотрим колебания системы с тремя степенями свободы, которая подвергалась воздействию по записи Газлийского землетрясения. Массы в системе приняты одинаковыми, а изгибная и сдвиговая жесткости постоянными по высоте. Основной период собственных колебаний системы был принят равным 0,65 с.
Задача о колебаниях системы решалась на ЭВМ по стандартной программе для решения систем линейных дифференциальных уравнений методом Рунге-Кутта. Масса гасителя принята равной 5% приведенной массы основной системы, что в данном случае составляет 7% верхней массы системы.
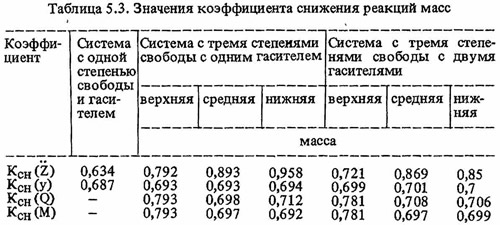
В табл. 5.3 даны значения коэффициента снижения реакций масс системы. Из таблицы видно, что коэффициент Ксн(у), определяемый по смещениям масс, очень мало отличается от соответствующего коэффициента для системы с одной степенью свободы (на 1%). Эффективность гасителя с точки зрения снижения ускорения в трехмассовой системе меньшая, чем эффективность гасителя в одномассовой системе.
В табл. 5.3 также приведены значения коэффициента Ксн для изгибающих моментов и поперечных сил, действующих в уровнях сосредоточения масс и в уровне опоры системы. В уровнях опоры и нижней массы эти коэффициенты близки по величине коэффициенту Ксн для одномассовой системы. Коэффициент Kсн(Q) для поперечной силы, действующей между верхней и средней массами и коэффициент Ксн(М) для изгибающего момента в уровне средней массы системы больше на 15,4% соответствующего коэффициента для одномассовой системы.
Таким образом, колебания рассмотренной системы по второй и третьей формам сказались на снижении эффективности гасителя только в верхней трети системы.
Была также рассчитана система с присоединенным к нижней массе системы дополнительным гасителем, настроенным на вторую частоту собственных колебаний системы. Значения коэффициента снижения реакций в основной системе приведены в табл. 5.3. Хотя дополнительный гаситель снизил общий уровень колебаний по второй форме, но максимальные значения реакций масс системы практически не изменились.